Question

Which of the following is an equation for the circle above?

Answer 1

Consider that the equation of a circle with center (h,k) and radius 'r' is given by,

`(x-h)^2+(y-k)^2=r^2`

Now, observe the given graph carefully.

It is seen that the circle has vertical extremes as (1,6) and (1,-2).

This forms the largest chord of the circle, that is, the diamter of the circle (d).

So the center will be the mid point of this diameter. The coordinates of the center can be calculated using the mid-point formula as follows,

`\begin{gathered} h=(x_1+x_2)/(2)=(1+1)/(2)=1 \\ k=(y_1+y_2)/(2)=(6+(-2))/(2)=(4)/(2)=2 \end{gathered}`

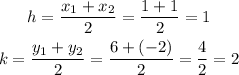
Thus, the center of the circle is (1,2).

The radius of the circle is the distance between the center and any one of the extreme points.

So apply the distance formula between (1,2) and (1,6) to obtain the radius (r) of the circle,

`\begin{gathered} r=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ r=\sqrt[]{(1-1)^2+(6-2)^2} \\ r=\sqrt[]{(0)^2+(4)^2} \\ r=\sqrt[]{(4)^2} \\ r=4 \end{gathered}`

Now, substitute these values in the standard form to get the equation of the circle,

`\begin{gathered} (x-1)^2+(y-2)^2=4^2 \\ (x-1)^2+(y-2)^2=16 \end{gathered}`

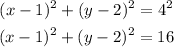
Thus, the equation of the given circle is obtained as,

`(x-1)^2+(y-2)^2=16`

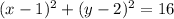
Therefore, option A is the correct choice.