Answer: MK = 15
Having that line KN is tangent to both circles, and point L being the center of circle L, we know that triangle KLM is a right triangle. Now, given that:
ML = 17
KL = 8
We can find MK through the Pythagorean theorem.
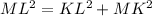
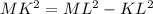
![MK^{}=\sqrt[]{ML^2-KL^2}](https://img.qammunity.org/2023/formulas/mathematics/college/mb636o33tds6gl3uq6pzzp1v2pq2qq0xhu.png)
![MK=\sqrt[]{17^2-8^2}](https://img.qammunity.org/2023/formulas/mathematics/college/maejuar6izg0q68omrm4cuuez555z41p25.png)
![MK=\sqrt[]{289-64}](https://img.qammunity.org/2023/formulas/mathematics/college/aoapofkeyrxh7wmn350hkp96a9xokbnwu3.png)
![MK=\sqrt[]{225}](https://img.qammunity.org/2023/formulas/mathematics/college/ps3eas3jgh59tdf3uzljfl8ndtbh30qvhz.png)
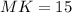
Therefore, MK = 15