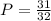Step-by-step explanation:
We have fair coins to be tossed in this experiment.
Note that each coin has a total outcome of 2 (that is head or tail).
For 5 of such coins, the total sample space would be 2^5, that is;

Note that when we want to conduct an experiment for "at least" one tail, this means we can get one tail or two, or three and so on. The least expected result is 1, and nothing less.
We first of all look at the chance of all outcomes being heads and that is;
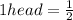

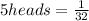
So the chance of getting ALL heads in 5 tosses would be 1/32.
The chance of getting 1 tail at least would be;
![P[tail]\ge1:1-(1)/(32)](https://img.qammunity.org/2023/formulas/mathematics/college/gdw92ijixlxpw1nkhfkv6fz9fpvg5h2hwn.png)
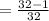
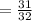
The probability of getting "at least" one tail therefore is;
ANSWER: