Answer:
x = -6 and x = 6
Step-by-step explanation:
If we have the difference of two perfect squares, we can factor the expression as:
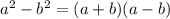
In this case, x² and 36 are perfect squares, so, we can factorize the expression as:
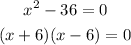
Now, if the multiplication of two numbers is 0, one of the numbers is equal to zero. It means that the possible solutions for the equation are:
x + 6 = 0
or
x - 6 = 0
So, solving for x, we get:
x + 6 = 0
x + 6 - 6 = 0 - 6
x = - 6
or
x - 6 = 0
x - 6 + 6 = 0 + 6
x = 6
Therefore, the roots of x² - 36 = 0 are:
x = -6 and x = 6