We know that diagonals bisect the angles because the figure is a rhombus. Also, the diagonals bisect each other at right angles.
We can find AMB using the diagonal property because AMB is a right angle, that is, it's equal to 90°.
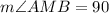
Let's find angle ABM using the interior angles theorem on the triangle AMB.
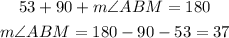
Given that diagonals bisect each other, then DM = BM = 6. And, MC = 12.-
Using the tangent function in triangle BMC to find angle MBC
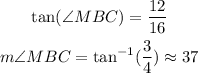
So, using the sum of angles, we have
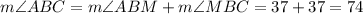
And the measure of angle DAB is
![undefined]()