Question

A body X' of mass 500g moving with a speed of 20m/sI collides with abody Y of mass 200g moving in the same direction with a speed of10m/s:. Given that the speed of body Y after the impact is 25m/scalculate the speed of body X.

Answer 1

Given:

The mass of the body X is m = 500 g =0.5 kg

The initial speed of the body X is

`v_(xi)=\text{ 20 m/s}`

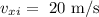
The mass of the body Y is m' = 200g = 0.2 kg

The initial speed of the body Y is

`v_(yi)=\text{ 10 m/s}`

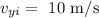
The final speed of the body Y is

`v_(yf)=\text{ 25 m/s}`

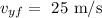
To find the final speed of the body X.

Step-by-step explanation:

The final speed of the body X can be calculated as

`\begin{gathered} mv_(xi)+m^(\prime)v_(yi)=mv_(xf)+m^(\prime)v_(yf) \\ v_(xf)=(mv_(xi)+m^(\prime)v_(yi)-m^(\prime)v_(yf))/(m) \\ =(0.5*20+0.2*10-0.2*25)/(0.5) \\ =14\text{ m/s} \end{gathered}`

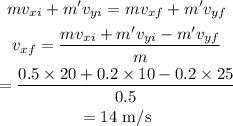
Thus, the speed of the body X after impact is 14 m/s.