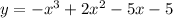Question

use cubic regression to find a function that fits the following points (1,-9),(2,-15),(3,-29),(-1,3) y=-x^3+ ?x^2 + ?x + ?

Answer 1

STEP - BY - STEP EXPLANATION

What to find?

A function that fits the given points.

Given:

(1,-9),(2,-15),(3,-29),(-1,3)

Step 1

Recall the general formula.

`y=ax^3+bx^2+cx+d`

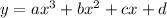
Step 2

Determine 4 equations by plugging in each of the given points.

(1, -9)

x=1 and y=-9

`\begin{gathered} -9=a(1)^3+b(1)^2+c(1)+d \\ \\ a+b+c+d=-9\text{ -----------\lparen1\rparen} \end{gathered}`

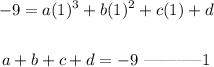
(2, -15)

x=2 and y=-15

`\begin{gathered} -15=a(2)^3+b(2)^2+c(2)+d \\ \\ 8a+4b+2c+d=-15\text{ ----------\lparen2\rparen} \end{gathered}`

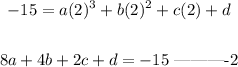
(3,-29)

x=3 and y=-29

`\begin{gathered} -29=a(3)^3+b(3)^2+c(3)+d \\ \\ 27a+9b+3c+d=-29--------(3) \end{gathered}`

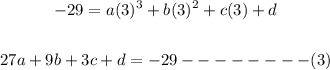
(-1, 3)

x=-1 and y=3

`\begin{gathered} 3=a(-1)^3+b(-1)^2+c(-1)+d \\ \\ -a+b-c+d=3\text{ ------------\lparen4\rparen} \end{gathered}`

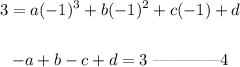
Step 3

Solve the for equations simultaneously.

Add equation

`\begin{gathered} 2b+2d=-6 \\ \\ b+d=-3-------(5) \end{gathered}`

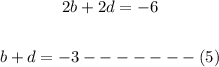
Step 4

From (1), Isolate for a

a=-9-b - c- 9

Substitute a=-9-b-c-d

8(-9-b-c -d)+ 4b + 2c +d =-15

27(-9-b-c-d)+9b + 3c +d =-29

-(-9-b-c-d)+b - c+ d=3

Step 5

Simplify

-4b-6c-7d-72=-15

-18b-24c-26d-243=-29

2b+2d+9=3

Step 6

Isolate b for 2b+2d+9=3

b = -d-3

Substitute b=-d-3

-4(-d-3)-6c-7d-72=-15

-18(-d-3)-24c-26d-243=-29

Step 7

Simplify

-6c-3d-60=-15 -----------------------(7)

-24c-8d-189=-29 ----------------(8)

Step 8

From (7) , isolate for c.

`c=-(d+15)/(2)-----(9)`

Step 9

Substitute c in (8)

4d - 9=-29

From the above d=-5

Step 10

Substitute in (10)

c=-5

Step 11

b=-d - 3

b=-(-5) - 3 =2

Step 12

Substitute the values in;

a=-9-b-c-d

a=-1

Step 13

Substitute the values into the general equation.

a=-1 b=2 c=-5 and d=-5

`y=-x^3+2x^2-5x-5`

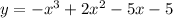
ANSWER

`y=-x^3+2x^2-5x-5`