Question

4. A) The pH of a solution is changed from pH 6 to pH 10. Does this reflect an increase or decrease in [H+]?B) By how much has the [H+] changed?

Answer 1

As a solution loses H+ ions its pH increases, i.e. the solution becomes more basic.

In this case, the solution goes from an acidic pH of 6 to a basic pH equal to 10, this means that the concentration of H+ in the solution decreases.

Now, to determine how much is the change of concentration we can apply the following formula:

`\begin{gathered} pH=-\log \lbrack H^+\rbrack \\ -pH=\log \lbrack H^+\rbrack \end{gathered}`

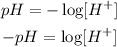
We can clear the H+ concentration by applying the logarithm rules. We have a base 10 logarithm so when clearing we will have:

`\lbrack H^+\rbrack=10^(-pH)`

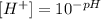
Now we replace the values of each pH and we will have the H+ concentration in each case.

`\begin{gathered} \lbrack H^+\rbrack_(pH=6)=10^(-6) \\ \lbrack H^+\rbrack_(pH=10)=10^(-10) \end{gathered}`

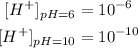
Therefore, the concentration difference will be:

`\begin{gathered} \Delta\lbrack H^+\rbrack=\lbrack H^+\rbrack_(pH=6)-\lbrack H^+\rbrack_(pH=10) \\ \Delta\lbrack H^+\rbrack=9.999*10^(-7) \end{gathered}`

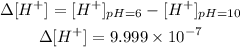
The change of concentration will be 9.999x10^-7