We have to divide the polynomial using synthetic division.
We then have to write the coefficients as:
-5 _| 1 -1 -38 -31 45
-5 30 40 -45
____________________
1 -6 -8 9 0
Then, we have the coefficients of a polynomial with one degree less than the dividend.
As our dividend is degree 4, our result is grade 3 and the coefficients 1, -6, -8, 9 and 0 correspond to a 3rd degree polynomial and the remainder:
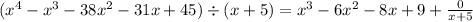
In this case, the remainder is 0, as the ast coefficient is 0.
Answer: x^3-6x^2-8x+9 [First option]