Given the function
![f(x)=\sqrt[]{3x-2}](https://img.qammunity.org/2023/formulas/mathematics/college/n4afvyb246b02riwr2xqdz1ldu350936px.png)
And the function
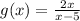
It is important to remember that the composition of functions can be expressed using the following notations:
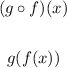
Therefore, in this case you can identify that the function f(x) must be inside of the function g(x). This means that you need to replace the variable "x" in the function g(x) with the function f(x).
Then, since you do not need to simplify the function, you get that the answer is:
![(g\circ f)(x)=\frac{2(\sqrt[]{3x-2})}{(\sqrt[]{3x-2})-5}](https://img.qammunity.org/2023/formulas/mathematics/college/ivkoefl8ruqs6nmz3fycyxwms2qxmwvure.png)