Question

The coordinates of the vertices of quadrilateral ABCD are A(-1, – 1), B(-3, 3), C(1,5), and D(5,2).Drag and drop the choices into each box to correctly complete the sentencesThe slope of AB isthe slope of BC isthe slope of CD isand the slope of AD isiQuadrilateral ABCD isbecause-2.2a parallelograma trapezoidneither a parallelogram nor a trapezoidboth pairs of opposite sides are parallelonly one pair of opposite sides is parallelneither pair of opposite sides is parallel

Answer 1

A pair of coordinates is given by (x,y)

The given coordinates of the vertices of the quadrilateral are:

A (-1, -1)

B (-3, 3)

C (1, 5)

D (5, 2)

To find the slope of a segment we can use the next formula:

`m=(y2-y1)/(x2-x1)`

Where m is the slope, and (x1, y1) and (x2, y2) are two points of the line.

The slope of AB:

`\begin{gathered} m=(3-(-1))/(-3-(-1))=(3+1)/(-3+1)=(4)/(-2) \\ m=-2 \end{gathered}`

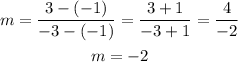
Thus, the slope of AB is -2.

The slope of BC:

`\begin{gathered} m=(5-3)/(1-(-3))=(5-3)/(1+3)=(2)/(4) \\ m=(1)/(2) \end{gathered}`

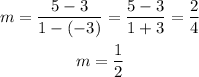
Thus, the slope of BC is 1/2.

The slope of CD:

`\begin{gathered} m=(2-5)/(5-1)=(-3)/(4) \\ m=-(3)/(4) \end{gathered}`

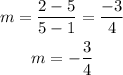
Thus, the slope of CD is-3/4.

The slope of DA:

`\begin{gathered} m=(-1-2)/(-1-5)=(-3)/(-6) \\ m=(1)/(2) \end{gathered}`

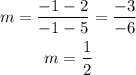
Thus, the slope of DA is 1/2.

Knowing the slopes of the sides, we can conclude that side BC is parallel to side DA, since they have the same slope 1/2 (remember that parallel lines have equal slope) but side AB is not parallel to CD since they have different slopes.

A parallelogram has two pairs of parallel sides, then quadrilateral ABCD is not a parallelogram.

A trapezoid is a quadrilateral that has one pair of parallel sides, thus quadrilateral ABCD is a trapezoid since only one pair of opposite sides is parallel.