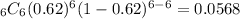Question

Need help with this question I got stuck on it d, e and f

Answer 1

d. 0.997

e. 0.414

f. 0.0568

EXPLANATION :

The binomial probability formula is :

`_nC_x(p)^x(1-p)^(n-x)`

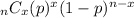
where :

n = number of trials or games

x = number of successful or game wins

p = probability of winning any game

From the problem, the probability of winning any game is p = 0.62

d. Probability that they win at least one game

Note that the sum of probability is always 1.

For example :

(probability of winning) + (probability of losing) = 1

So we can say that the probability of winning at least one game (1, 2, 3, 4, 5, and 6) + the probability of NOT winning any game (0) is 1

From c, the probability that they do NOT win any of the games is 0.00301

Then :

`\begin{gathered} (\text{ probability of winning atleast 1})+(\text{ probability of NOT winning})=1 \\ (\text{ probabilit of winning atleast 1})+0.00301=1 \\ =1-0.00301 \\ =0.997 \end{gathered}`

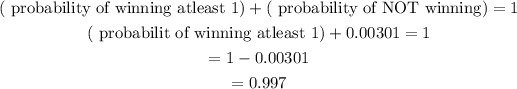
The answer is 0.997

e. Probability that they win at most three of the games.

That's when x ≤ 3

Using the formula above :

`\begin{gathered} \text{ x = 0} \\ _6C_0(0.62)^0(1-0.62)^(6-0)=0.0030 \\ \\ \text{ x = 1} \\ _6C_1(0.62)^1(1-0.62)^(6-1)=0.0295 \\ \\ \text{ x = 2} \\ _6C_2(0.62)^2(1-0.62)^(6-2)=0.1202 \\ \\ \text{ x = 3} \\ _6C_3(0.62)^3(1-0.62)^(6-3)=0.2616 \end{gathered}`

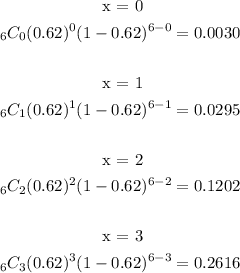
The sum is 0.0030 + 0.0295 + 0.1202 + 0.2616 = 0.4143

The probability is 0.4143

f. Probability that they win all of the games.

That's when x = 6

`_6C_6(0.62)^6(1-0.62)^(6-6)=0.0568`