Question

1. Describe the similarities and differences among the following experiments. (a) Slips of paper are marked with the numbers 1, 2, 3, 4, and 5 and placed into a box. After being mixed, two slips are drawn simultaneously. (b) Slips of paper are marked with the numbers 1, 2, 3, 4, and 5 and placed into a box. After being mixed, one slip is drawn then put back into the box, then a second slip is drawn. (c) Slips of paper are marked with the numbers 1, 2, 3, 4, and 5 and placed into a box. After being mixed, one slip is drawn and not put back into the box, then a second slip is drawn. 2. One urn contains four BLUE balls marked 1, 2, 3, and 4, and a second urn contains five GREEN balls marked 1, 2, 3, 4, and 5. One ball is selected from each urn. (a) What is the sample space? (b) List the outcomes in the eventsE = { the number on the BLUE ball is even or the sum of the two balls is 5 } , F = { the number of the GREEN ball is even and the sum of the two balls is 5 } .(c) Find the probability ofEand the probability ofF.

Answer 1

When picking a ball from the blue urn, the possible outcomes are

`B=\lbrace B1,B2,B3,B4\rbrace`

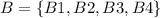
Similarly, in the case of the other urn,

`G=\lbrace G1,G2,G3,G4,G5\rbrace`

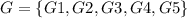
Therefore, the sample space of the experiment that consists of selecting one ball from each urn is

`\Rightarrow S=\lbrace(B1,G1),(B1,G2),...,(B1,G5),(B2,G1),...,(B4,G4),(B4,G5)\rbrace\rightarrow20\text{ elements in total}`

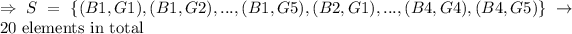
The answer to part a) is set S shown above.

b)

If the number on the blue ball is even, any ordered pair whose first coordinate is B2 or B4 is within set E. On the other hand,

`\begin{gathered} 1+4=5 \\ 4+1=5\rightarrow\text{ already counted when Blue is even} \\ 2+3=5\rightarrow\text{ already counted when BLUE is even} \\ 3+2=5 \end{gathered}`

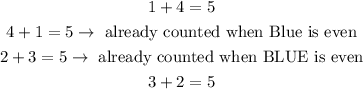
Then, set E is

As for set F,

When the number of the green ball is even G2 or G4. Then, if additionally, the sum of the two balls is 5,

`\begin{gathered} 1+4=5\rightarrow Green\text{ is ven} \\ 2+3=5 \\ 3+2=5\rightarrow\text{ green is even} \\ 4+1=5 \end{gathered}`

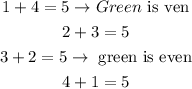
Therefore, out of the 10 outcomes in which G2 or G4, only 2 of them satisfy the second condition (sum equal to 5). Thus, set F is

`F=\lbrace(B1,G4),(B3,G2)\rbrace\rightarrow\text{ 2 elements}`

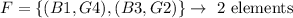
c) Finally, the corresponding probabilities of E and F are

`\begin{gathered} P(E)=(12)/(20)=(3)/(5) \\ P(F)=(2)/(20)=(1)/(10) \end{gathered}`

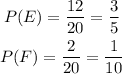
The probability of E is 3/5 and the probability of F is 1/10