The formula to calculate the confidence interval is
![P\pm z*\sqrt[]{(P(1-P))/(n)}](https://img.qammunity.org/2023/formulas/mathematics/college/hfz92vfyi97g4ss6de7ijdcw0uckuoy8rc.png)
Where

We can calculate the sample proportion by
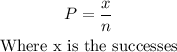
The parameters are
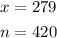
Using an online calculator, the z-score for a 90% confidence interval is 1.645.
Therefore, we can calculate P to be:
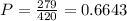
Hence, we can calculate calculate the confidence interval by substituting the values
![\begin{gathered} =0.6643\pm1.645\sqrt[]{(0.6643(1-0.6643))/(420)} \\ =0.6643\pm1.645(0.023) \\ =0.6643\pm0.0378 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/efh7lg667l0kzz4zxioy43bqvqryft8f0g.png)
Therefore, the lower limit of the confidence interval is
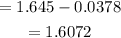
The lower limit of the confidence interval is 1.6072
Therefore, the upper limit of the confidence interval is
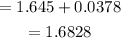
Therefore, the upper limit of the confidence interval is 1.6828