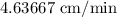1 Answer

Mohammed Sajid · Answer 1 · 2023-10-02T12:24:08+0000

Solution:

The area of a triangle is expressed as

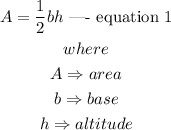
$\begin{gathered} A=(1)/(2)bh\text{ ---- equation 1} \\ where \\ A\Rightarrow area \\ b\Rightarrow base \\ h\Rightarrow altitude \end{gathered}$

From equation 1, taking the derivative of A with respect to t, we have

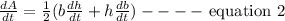
$(dA)/(dt)=(1)/(2)(b(dh)/(dt)+h(db)/(dt))----\text{ equation 2}$

Given that the altitude is increasing at a rate of 2.5 cm/minute while the area is increasing at a rate of 5 square cm /minute, this implies that

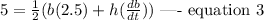
$5=(1)/(2)(b(2.5)+h((db)/(dt)))\text{ ---- equation 3}$

To evaluate the rate at which the base is changing when the altitude is 8.5 cm and the area is 84 square cm, we have

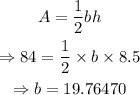
$\begin{gathered} A=(1)/(2)bh \\ \Rightarrow84=(1)/(2)* b*8.5 \\ \Rightarrow b=19.76470 \end{gathered}$

By substitution, we have

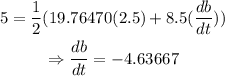
$\begin{gathered} 5=(1)/(2)(19.76470(2.5)+8.5((db)/(dt))) \\ \Rightarrow(db)/(dt)=-4.63667 \end{gathered}$

Hence, the base changes at

$4.63667\text{ cm/min}$

Please log in or register to add a comment.