Question

Part A: If triangle ABC is dilated using centerand scale factor, what is the length of A'B'?units.The length of A'B' isnow your answer. Question #5Part B: What do the properties of dilations tell you about angle B’?

Answer 1

Using the center and a scale factor of 3/2, we can say that the length A'B' will be

`A^(\prime)B^(\prime)=f\cdot AB`

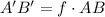
Where f is the scale factor, then

`\begin{gathered} A^(\prime)B^(\prime)=(3)/(2)\cdot4 \\ \\ A^(\prime)B^(\prime)=3\cdot2 \\ \\ A^(\prime)B^(\prime)=6 \end{gathered}`

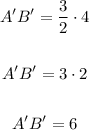
The length of A'B' is 6 units.

One of the properties of dilations is that the angles are always the same. Therefore the angle B' is the same angle as B.