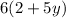Question

12 + 30y how can i factor the expressions

Answer 1

We are given the expression;

`12+30y`

To factor a given expression, we take each part separately and look for any factors that can divide both without remainders.

Looking at the first one;

`12=2*2*3`

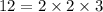
And then the other one;

`30y=2*3*5* y`

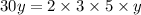
Notice that 2 and 3 afre common factors (that is 2 times 3 = 6).

Hence, we can factor out 6 from both parts of this expression as follows;

`(12)/(6)+(30y)/(6)`

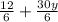
Or if you want it to look more simplified (for the sake of understanding the steps better);

`\begin{gathered} ((2*2*3))/(2*3)+((2*3*5* y))/(2*3) \\ =2+(5* y) \\ =2+5y \end{gathered}`

This means we can now re-write after factoring out 6;

`6(2+5y)`

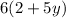
That is;

`12+30y=6(2+5y)`

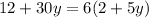
ANSWER:

`6(2+5y)`