The solution set is given by solving the equation:
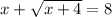
Subtract x from both sides of the equation:
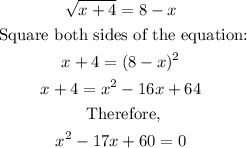
To factorize the quadratic equation, Find two numbers such that their product is 60 and their sum is -17.
The two numbers are 5 and 12.
Hence,
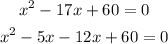
Factorizing the equation we have:
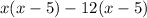
Hence,
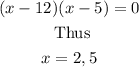
Check if x = 2 the solutions are extraneous:
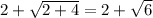
Hence x=2 is an extraneous solution
Check if x = 5 the solutions are extraneous:
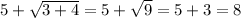
Hence x=5 is a solution
Therefore, the solution set is { 5 }