Question

Fill out the table of values and select whether each function is odd, even or neither. You may only submit once the tables of values have been filled out correctly.

Answer 1

We have three functions.

We have to calculate the values of y for different values of x.

We start with f(x) = |x| - 1.

We can calculate the different values as:

`\begin{gathered} x=-2\Rightarrow f(-2)=|-2|-1=2-1=1 \\ x=-1\Rightarrow f(-1)=|-1|-1=1-1=0 \\ x=0\Rightarrow f(0)=|0|-1=0-1=-1 \\ x=1\Rightarrow f(1)=|1|-1=1-1=0 \\ x=2\Rightarrow f(2)=|2|-1=2-1=1 \end{gathered}`

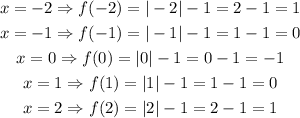
We now calculate the values for f(x) = x^5 - 1:

`\begin{gathered} x=-2\Rightarrow f(-2)=(-2)^5-1=-32-1=-33 \\ x=-1\Rightarrow f(-1)=(-1)^5-1=-1-1=-2 \\ x=0\Rightarrow f(0)=0^5-1=0-1=-1 \\ x=1\Rightarrow f(1)=1^5-1=1-1=0 \\ x=2\Rightarrow f(2)=2^5-1=32-1=31 \end{gathered}`

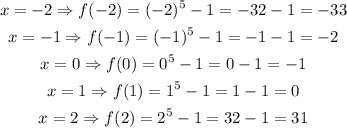
Finally, we calculate the values for f(x) = x^3 - x^7:

`\begin{gathered} x=-2\Rightarrow f(-2)=(-2)^3-(-2)^7=-8-(-128)=120 \\ x=-1\Rightarrow f(-1)=(-1)^3-(-1)^7=-1-(-1)=0 \\ x=0\Rightarrow f(0)=0^3-0^7=0 \\ x=1\Rightarrow f(1)=1^3-1^7=1-1=0 \\ x=2\Rightarrow f(2)=2^3-2^7=8-128=-120 \end{gathered}`

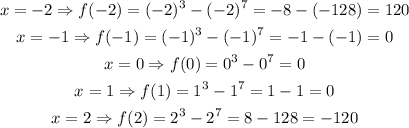
We now have to check if the functions are odd, even or neither.

Even functions have to satisfy the following rule:

`f(x)=f(-x)`

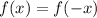
We can use the tables to check this condition: we look at the value of f(-2) and f(2) and see if they are equal or not. The same has to be done for f(-1) and f(1).

If the function is even, we have to have f(-2) = f(2) and f(-1) = f(1).

The only function that satisfies this condition is f(x) = |x| - 1, so this function is even:

`\begin{gathered} f(-2)=1=f(2) \\ f(-1)=0=f(1) \end{gathered}`

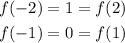
The other functions are not even.

We now check if the remaining functions are odd or not.

Odd functions satisfy the following condition:

`f(x)=-f(-x)`

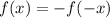
In this case, we check the values of f(x) for x = -2 and x = -1 and see if they are the opposite values for f(x) when x = 2 and x = 1 respectively.

The function that satisfy this condition is f(x) = x^3 - x^7:

`\begin{gathered} f(-2)=120=-(-120)=-f(-2) \\ f(-1)=0=-0=-f(1) \end{gathered}`

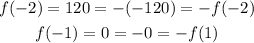
Then this function is odd.

The remaining function is neither even nor odd.

Answer:

We can complete the table as