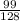Solution:
In the toss of a coin, the possible outcome is either head (H) or tail (T).


To get between 3 and 6 heads, inclusive, the following outcomes holds;

Probability of 3H, 7T using binomial distribution for the arrangement of the outcomes
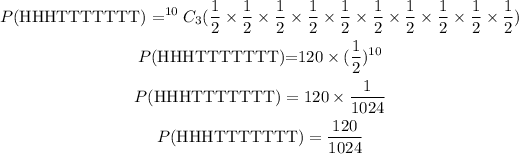
Probability of 4H, 6T using binomial distribution for the arrangement of the outcomes

Probability of 5H, 5T using binomial distribution for the arrangement of the outcomes
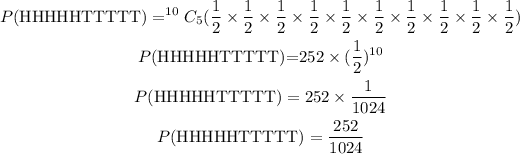
Probability of 6H, 4T using binomial distribution for the arrangement of the outcomes
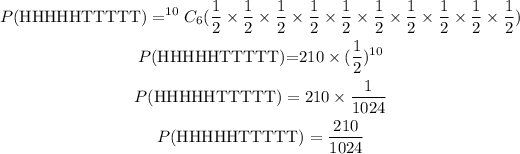
The probability of getting between 3 and 6 heads inclusive in 10 tosses of a coin will be the sum of the probabilities gotten.
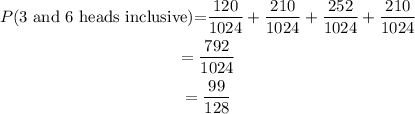
The probability of getting between 3 and 6 heads inclusive in 10 tosses of a coin is