In this question, we need to find the probability of an event in which the final result depends on one of the events to happen. It is a conditional probability.
We have a bag with the following amount of different candies:
• 5 yellows candies
,
• 11 red candies
,
• 4 green candies
,
• 12 blue candies
,
• 7 brown candies.
If we add all of these candies, we have a total of 39 candies.
Now, we need to find the probability of pulling a green candy from the bag is:
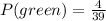
Since Julie ate one of the candies, there will be 38 candies in the bag after that event. Now the probability of pulling a blue candy is:
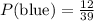
Hence, the probability, in this case, is the product of both previous probabilities as follows:
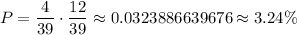
If we round the probability to the nearest percent, we have that the probability will be, approximately, 3%.
In summary, we have that the probability, to the nearest percent, that Julie pulls a green M and M from the bag, eats it, then pulls a blue candy from the bag is, approximately, 3% (option C.)