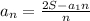Question

na+an)The formula S-2. gives the partial sum of an arithmetic sequence. What is the formula solved for an?2S-a, noa,nan2S+annO an-2S+ a13+an-2-an+n

Answer 1

To solve the formula for an, we need to start from it and try to get an alone in one side.

So, firstly, let's copy the formula and invert the sides so an gets to the left side:

`\begin{gathered} S=(n(a_1+a_n))/(2) \\ (n(a_1+a_n))/(2)=S \end{gathered}`

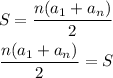
So, first, let's get rid of the denominator by multiplying both sides by 2, which will cancel it out:

`\begin{gathered} (n(a_1+a_n))/(2)=S \\ 2\cdot(n(a_1+a_n))/(2)=2\cdot S \\ n(a_1+a_n)=2S \end{gathered}`

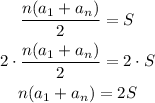
Now, let's apply the distibutive property on the parenthesis:

`\begin{gathered} n(a_1+a_n)=2S \\ na_1+na_n=2S \end{gathered}`

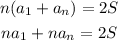
Since the first term of the left side has no an, we can get it to the other side, which we will do by substracting na1 from both sides:

`\begin{gathered} na_1+na_n=2S \\ na_1-na_1+na_n=2S-na_1 \\ na_n=2S-na_1 \end{gathered}`

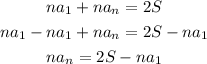
Finally, we can divide both sides by n to cancel it out on the left side:

`\begin{gathered} na_n=2S-na_1 \\ (na_n)/(n)=(2S-na_1)/(n) \\ a_n=(2S-na_1)/(n) \end{gathered}`

As we can see, the first option is almost the same, but n and a1 are switched. However, since it is a multiplication, they are equivalent.

So, the correct alternative is:

`a_n=(2S-a_1n)/(n)`