Question

How would you get the equation of the line in slope-intercept form?

Answer 1

`y=-x-6`

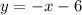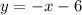
1) We're going to tackle this question by examining the graph and picking two points from that line. Namely, (-5,-1) and (3,-9)

2) So let's plug them into the slope formula, so that we can find the slope, i.e. the measure of how steep is that line:

`m=(y_2-y_1)/(x_2-x_1)=(-9-(-1))/(3-(-5))=(-9+1)/(3+5)=(-8)/(8)=-1`

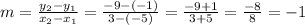
3) The next step is to find the y-intercept. We can see in the graph that the line intercepts the y-axis at y=-6. But let's test it by finding the linear coefficient "b" algebraically:

`\begin{gathered} (-5,-1),\text{ m=-1} \\ y=mx+b \\ -1=-1(-5)+b \\ -1=5+b \\ -1-5=5-5+b \\ b=-6 \end{gathered}`

Finally, we can write out the equation of the line in the slope-intercept form:

`y=-x-6`