Given:
The ratio is given as,
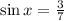
The x is in the second quadrant.
The objective is to find the value of sin2x, cos2x and tan2x.
Step-by-step explanation:
To find cos x :
Using the trigonometric identity,
![\begin{gathered} \sin ^2x+\cos ^2x=1 \\ \cos ^2x=1-\sin ^2x \\ \cos x=\sqrt[]{1-\sin^2x}\text{ . . . . .(1)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/64jcq0hpwlkl2wwukul098g8sf3jk1gh7u.png)
On plugging the given values in equation (1),
![\begin{gathered} \cos x=\sqrt[]{1-((3)/(7))^2} \\ =\sqrt[]{1-(9)/(49)} \\ =\sqrt[]{(49-9)/(49)} \\ =\pm\frac{\sqrt[]{40}}{7} \\ =\pm\frac{2\sqrt[]{10}}{7} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mmxxcx2lq44obvd6o8roebnp4tpx1ytu0a.png)
Since x lies in the second quadrant,
![\cos x=-\frac{2\sqrt[]{10}}{7}](https://img.qammunity.org/2023/formulas/mathematics/college/4b96bts8r7iw0vvsj43df575t4ocllafv7.png)
a)
To find sin(2x):
The general formula to find sin(2x) is,
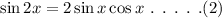
On plugging the obtained values in equation (2),
![\begin{gathered} \sin 2x=2((3)/(7))(-\frac{2\sqrt[]{10}}{7}) \\ =-\frac{12\sqrt[]{10}}{49} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/oetm1614xbmczmqf7yo5emanc7chswvb1m.png)
Hence, the value of sin(2x) is (-12√10)/49.
b)
To find cos (2x):
The general formula of cos(2x) is,
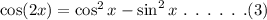
On plugging the obtained values in equation (3),
![\begin{gathered} \cos (2x)=(-\frac{2\sqrt[]{10}}{7})^2-((3)/(7))^2 \\ =(4*10)/(49)-(9)/(49) \\ =(40-9)/(49) \\ =(31)/(49) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/kubx1brhez5r3pqh6xsqw307jjkikpct0s.png)
Hence, the value of cos(2x) is 31/49.
c)
To find tan(2x):
The general formula of tan(2x) is,
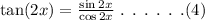
On plugging the obtained values in equation (4),
![\begin{gathered} \text{tan}(2x)=\frac{\frac{-12\sqrt[]{10}}{49}}{(31)/(49)} \\ =-\frac{12\sqrt[]{10}}{31} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6ch3vj910huf9jv422q4asrks0uzhgd1e0.png)
Hence, the value of tan(2x) is (-12√10/31).