Question

For the function, the vertex of the function’s graph is given. Find the unknown coefficients.y=x^2+bx+c;(-5,6)

Answer 1

The Vertex of a Parabola

Given a function of the form:

`f(x)=ax^2+bx+c`

Its graph has a shape known as a parabola. The vertex of a parabola is the point of its maximum or minimum value.

The x-coordinate of the vertex is given by:

`x_v=-(b)/(2a)`

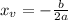
Given the function:

`f(x)=x^2+bx+c`

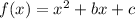
It's evident that a =1, but we don't have b or c.

Calculating xv:

`x_v=-(b)/(2)`

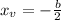
We are given this value is -5, thus:

`\begin{gathered} -(b)/(2)=-5 \\ \text{Solving for b:} \\ b=10 \end{gathered}`

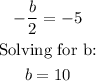
Substitute the value of b in the function:

`y=x^2+10x+c`

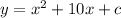
We are also given the value of y = 6 when x=-5. Substituting:

`6=(-5)^2+10(-5)+c`

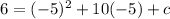
Operating:

`\begin{gathered} 6=25-50+c \\ 6=-25+c \\ c=31 \end{gathered}`

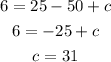
The required coefficients are b = 10 and c = 31