- The lateral area is given by the formula:

Where:
Perimeter = 15 + 17 + side triangle
Height = 26 in26
First, we find the length of other side using the pythagoras theorem:
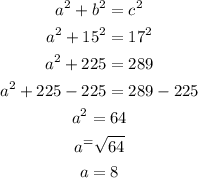
Therefore the perimeter is:
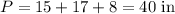
And the lateral area is:

- The surface area is given by
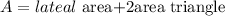
Then, the area of the triangle is:
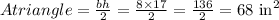
So, the surface area is:
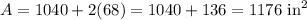
Answer:
Lateral area = 1040 in^2
Surface area = 1176 in^2