Question

The resistance, of a wire varies directly as its length and inversely as the square of its diameter. The resistance of a wire 4900 ft long with a diameter of 0.27 inches 17072 ohms, what is the resistance of 2700 ft of the same type of wire with a diameter of 0.19 inches? (Leave k in fraction form or round to at least 3 decimal places Round off your final answer to the nearest hundredth)

Answer 1

k = 0.25399 ohms.in²/ft

R = 18996.48 ohms

Step-by-step explanation

The resistance, of a wire varies directly as its length and inversely as the square of its diameter implies

`\begin{gathered} R\propto(l)/(d^2) \\ \\ \Rightarrow R=(kl)/(d^2) \end{gathered}`

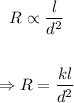
Where R is the resistance of the wire, l is the length, d is the diameter, and k is a constant of proportionality.

Putting R = 17072 ohms, l = 4900 ft, and d = 0.27 inches, we have:

`\begin{gathered} 17072\text{ }ohms=\frac{k*4900ft}{(0.27\text{ }in)^2} \\ \\ k=\frac{17072\text{ }ohms*(0.27\text{ }in)^2}{4900\text{ }ft}=\frac{1244.5488\text{ }ohms.in^2}{4900\text{ }ft} \\ \\ k=0.25399\text{ }ohms.in^2\text{/}ft \end{gathered}`

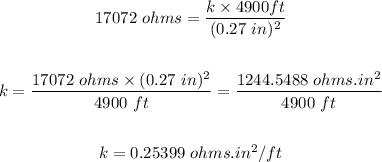
To find the R, put l = 2700 ft, and d = 0.19 inches:

`\begin{gathered} R=\frac{0.25399\text{ }ohms.in^2\text{/}ft*2700\text{ }ft}{(0.19\text{ }in)^2} \\ \\ R=\frac{685.773\text{ }ohms.in^2}{0.0361\text{ }in^2} \\ \\ R=18996.48\text{ }ohms \end{gathered}`