Question

A small publishing company is planning to publish a new book. The production costs will indude one-time foxed costs (such as editing) and variable costs (suchas printing). The one-time foxed costs will total $41,446. The variable costs will be $11.50 per book. The publisher will sell the finished product to bookstories at a price of $24.75 per book. How many books must the publisher produce and sell so that the production costs will equal the money from sales?

Answer 1

The production costs include fixed and variable costs, it can be written as:

`\begin{gathered} \text{Production costs=fixed costs+variable costs} \\ \text{Production costs=\$41446+\$11}.50\cdot x \end{gathered}`

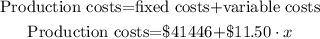
Where x is the number of produced books.

Now, the money from sales can be written as:

`Sales=x\cdot\text{ \$24.75}`

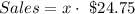
To find how many books must the publisher produce and sell so that the production costs will equal the money from sales, you have to equal production costs to money from sales and solve for x:

`\begin{gathered} \text{Production costs=Money from sales} \\ 41446+11.50x=24.75x \\ \text{Subtract 11.50x from both sides} \\ 41446+11.50x-11.50x=24.75x-11.50x \\ 41446=13.25x \\ \text{Divide both sides by 13.25} \\ (41446)/(13.25)=(13.25x)/(13.25) \\ \text{Simplify} \\ 3128=x \\ \text{And reorder terms} \\ x=3128 \end{gathered}`

Thus, the number of books the publisher has to produce and sell is 3128.