Given the functions
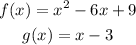
You have to find the quotient between both functions, that is (f/g)(x)

To solve this division, the first step is to factor the numerator.
To factor the quadratic function, you have to find a value or values whose sum is -6 and their product is 9.
The number that fulfills both characteristics is -3
The factor of f(x) is (x-3) and its factorized form is:

You can rewrite the quotient as follows:
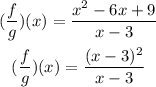
The next step is to simplify the expression:
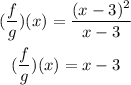
The result is (f/g)(x)=x-3