Given an Inverse Variation in which "y" varies inversely as "x", you need to remember the form of an Inverse Variation Equation:

Where "k" is the Constant of variation.
In this case, you know that when:

The value of "y" is:
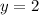
Then, you can substitute values into the equation and solve for "k":
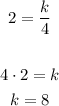
Therefore, the equation describing the relationship given in the exercise has this form:
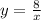
Hence, the answer is:
- Equation:
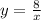
- The numerator is:
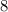
- The denominator is:
