Question

Find the change in the car is kinetic energy from the bottom of the hill to the top of the hill

Answer 1

The change in kinetic energy of the car as it drives up the hill is 3.53 x
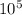`10^(5)` J.

The work-energy principle states that the net work done on an object is equal to the change in its kinetic energy.

To find the change in the car's kinetic energy from the bottom of the hill to the top, we can apply the work-energy principle that states the change in kinetic energy (ΔKE) equals the net work done on the object:

ΔKE = Work by the engine + Work by friction

According to the problem, the work done by the engine is 6.64 x
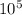`10^(5)` J and the work done by friction is -3.11 x
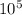`10^(5)` J. Putting these values into our equation gives us:

ΔKE = (6.64 x 
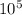`10^(5)` J) - (3.11 x
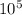`10^(5)` J) = 3.53 x
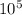`10^(5)` J

Therefore, the change in the car's kinetic energy as it drives up the hill is 3.53 x
`10^(5)` J.

Answer 2

We will determine the energy as follows:

`F=((6.64\ast10^5)-(3.11\ast10^5))/(16.2)\Rightarrow F=21790.12346...`
`\begin{gathered} F=ma\Rightarrow21790.12346=m\ast9.8m/s^2 \\ \\ \Rightarrow m=2223.481985... \end{gathered}`

Now, we determine the velocity:

`v=\sqrt{(2(21790.12346))/(2223.481985)}\Rightarrow v=4.427188725`

Finally we will have:

`\begin{gathered} \Delta k=(1)/(2)mv^2\Rightarrow\Delta k=(1)/(2)(2223.481985)(4.427188725)^2 \\ \\ \Rightarrow\Delta k=21790.12346 \end{gathered}`

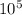So, the kinetic energy was approximately 21790.1 J.