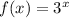So we must find an exponential function. The general form of these functions is:
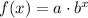
By using the table provided by the question we can find the values of a and b and thus the expression of the function. In this case we can take two pairs of values from the table. On one hand we have that x=1 and f(1)=3, on the other hand we have x=2 and f(2)=9. Using the former formula we can build two equations:
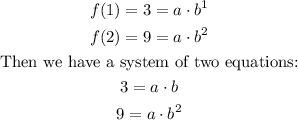
Let's use the first one:
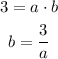
Now we substitute 3/a in place of b in the second equation:
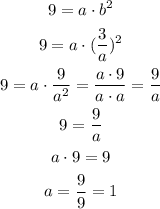
So a=1 and since we found that b=3/a then b=3. Then the exponential function that we are looking for is: