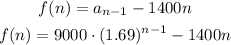SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given equation for explicit formula

STEP 2: Write the given details
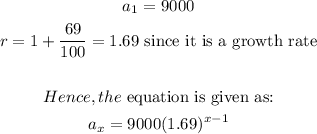
STEP 3: Get the explicit equation for f(n)
n = x
Substitute n for x in the equation in step 2.
Therefore, the explicit equation is given as:
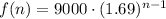
STEP 4: Answer part B
To get how many lionfish in the bay after 6 years
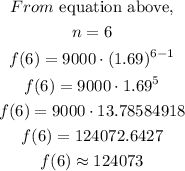
Hence, there will be approximately 124073 lionfish
STEP 5: Get the recursive formula
1400 lionfish was removed per year, this gives an equation defined below:
Recursive formula is given as
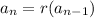
Since we know that the difference each year is 1400, this gives the equation below:
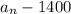
By substitution, the recursive formula will be given by:
Since 1400 is removed each year, we have: