Given:
Face value, P = $10000
Time, t = 10 years
Rate, R = 6.4% = 0.064
Let's solve for the following:
• 1) Calculate the semi-annual interest payments.
Apply the formula:
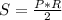
Thus, we have:

The semi-annual interest payment is $320
• (2) Calculate the present value of the payments.
To find the present value, apply the formula:
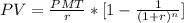
Where:
r = 0.065/2 = 0.0325
n is the number of periods = 10 x 2 = 20
PMT = 320
Thus, we have:

The present value of the payments is $4652.59
3) Calculate the present value of the bond at maturity.
Take the formula:
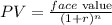
Thus, we have:

The present value of the bonds at maturity is $5274.71
• 4) Find the price of this bond.
To find the price f this bond, we have:
Price of bond = Present value of payments + Present value at maturity
Price of bond = $4652.59 + $5274.71
Price of bond = $9927.30
The price of this bond is $9,927.30
5) To find the current yield, apply the formula:
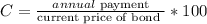
Thus, we have:
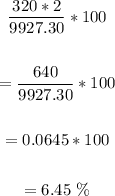
The current yield is 6.45%
ANSWER:
1) $320
2) $4,652.59
3) $5,274.71
4) $9,927.30
5) 6.45%