Given:
• Final amount, A = $80,000
,
• Time, t = 10 years
,
• Interest rate, r = 4.0% = 0.04
,
• Number of times compounded, n = monthly = 12 times a year.
Let's find the amount she should invest to achieve her goal.
Here, we are to find the principal, P.
Apply the compound interest formula:
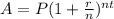
Where:
A = $80,000
r = 0.04
n = 12
t = 10 years
Substitute values into the formula and solve for P:
We have:

Divide both sides by 1.49083:
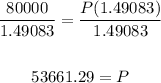
Therefore, the amount she should invest is $53,661.29
ANSWER:
$53,661.29