SOLUTION:
Case: Measure of central tendency
Method:
1. The Mean
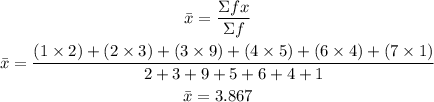
2. The Median
The position of the median (middle) number of children per family is 15th.
The median= 4 per family
3. The mode.
The family with the highest number of children occurs 9 times.
The highest number has 3 children per family
Final answer:
The mean = 3.867 children per family
The median= 4 children per family
The mode= 3 children per family