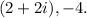Given:
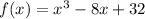
The zero is (2-2i).
Required:
We need to find the zeros of the given function f(x).
Step-by-step explanation:
The zeros of the function f(x) is 2-2i.
Use the synthetic method.
The given f(x) can be written as follows.
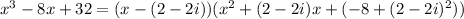
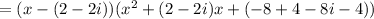
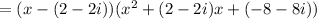
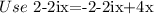
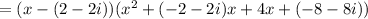
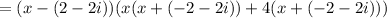
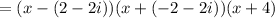
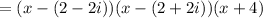
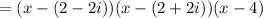
The zeros of the function f(x) are (2-2i), (2+2i), and (-4).
Final answer: