Given:
The final amount is given as A = ₱5,000.
The number of yeats is T = 6.
The interest is compounded at the end of each 3 months, n = 4 per year.
The rate of interest is r = 8% = 0.08.
The objective is to find the amount deposited at the beginning.
Step-by-step explanation:
The general formula to find the compound interest is,
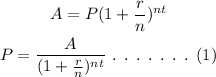
On plugging the given values in equation (1),
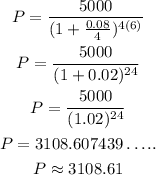
Hence, the amount to be deposited is ₱3108.61.