Answer:
K'(-3, 6)
Explanation:
From the graph, the coordinates of G, H, and K are: G(1,3), H(6,0), and K(6,3).
If a point (x,y) is rotated 90 degrees counterclockwise about the origin, the transformation rule is:
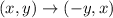
Thus, the coordinates of the image points of the triangle GHK are:
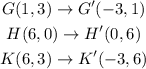
The coordinates of the image of the point K is (-3,6).