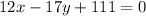Given:
The line passes through the point (-5, 3) and is parallel to the line through (9, 6) and (-8, -6).
To find:
The line of the equation.
Step-by-step explanation:
Using the two points (9, 6) and (-8, -6),
Finding the slope,
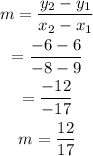
Using the point-slope formula,
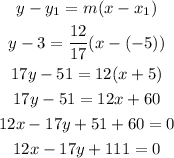
Therefore, the equation of the line is,
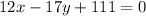
Final answer:
The equation of the line is,