We are asked to determine the coefficient of friction of the 5 kg block. The free-body diagram of the system is the following:
Where:

Now, we add the forces in the horizontal direction:
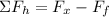
According to Newton's second law we have that the sum of forces is equal to the product of the mass and the acceleration, therefore, we have:
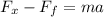
The x-component of the applied force is determined using the function cosine:
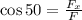
Now, we multiply both sides by "F":
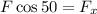
Substituting in the horizontal sum of forces:
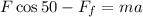
Now, we solve for the friction force. First, we subtract "Fcos50" from both sides:
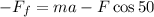
Now, we multiply both sides by -1:
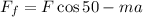
Now, we substitute the values:
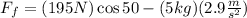
Solving the operations:
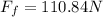
Now, we use the following formula that relates the friction force and the coefficient of friction:
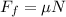
Where:
Now, we determine the normal force by adding the vertical forces:
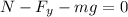
the sum of forces is equal to zero since there is no acceleration in the vertical direction. Now, we solve for the normal force by adding "mg" to both sides:
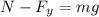
Now, we add the y-component of the force:
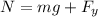
To determine the y-component of the force we use the function sine:
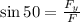
Now, we multiply both sides by "F":
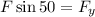
Substituting in the formula for the normal force:
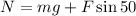
Now, we substitute the values:
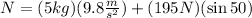
Solving the operations:
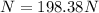
Now, we substitute in the formula for the friction force:
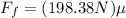
Now, we divide both sides by 198.38:
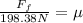
Now, we substitute the value of the friction force:
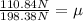
Solving the operations:
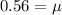
Therefore, the coefficient of friction is 0.56