Question

For a quadratic equation with discriminant (-6)^2-4 x 4 x 3 identify the number of solutions and their type(s)

Answer 1

Discriminant for a quadratic equation is given as

`D=b^2-4ac`

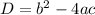
If the discriminant D = 0, it has one real root.

If D > 0, it has two real roots

If D < 0, it has no real root.

From the question, they have given us

`\begin{gathered} b^2-4ac\text{ = }(-6)^2-4*4*3 \\ \text{Now we will check what }(-6)^2-4*4*3\text{ will give } \\ (-6)^2-4*4*3 \\ 36-48 \\ -12\text{ } \end{gathered}`

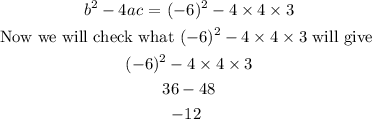
So since D is negative that is less than zero, it has no real roots and 2 complex solutions

So, our answer is 2 complex solutions and no real roots