Question

Need help with mixture problems with system of linear please see attached picture

Answer 1

The Solution:

Let the first mechanic rate per hour be x and the second mechanic rate per hour be y.

Representing the given problem in equations, we have:

`\begin{gathered} 20x+5y=1800\ldots\text{eqn}(1) \\ x+y=165\ldots\text{eqn}(2) \end{gathered}`

We are asked to find the values of x and y.

Step 1:

From eqn(2), find y.

`y=165-x\ldots\text{eqn}(3)`

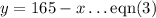
Step 2:

putting eqn(3) into eqn(1), we get

`20x+5(165-x)=1800`

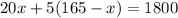
Simplifying, we get

`20x+825-5x=1800_{}`

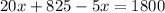
Collecting the like terms, we get

`\begin{gathered} 20x-5x=1800-825 \\ 15x=975 \end{gathered}`

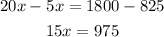
Dividing both sides by 15, we get

`x=(975)/(15)=65=\text{ \$65}`

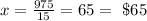
Step 3:

Substituting 65 for x in eqn(3), we get

`\begin{gathered} y=165-65 \\ y=100=\text{ \$100} \end{gathered}`

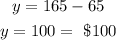
Therefore, the correct answers are:

The first mechanic charges $65 per hour.

The second mechanic charges $100 per hour.