Question

A bottling company uses a filling machine to fill plastic bottles with cola. The bottles are supposed to contain 300 milliliters (ml). In fact, the contents vary according to a Normal distribution with mean = 298 ml and standard deviation = 3 ml.What is the probability that the contents of a randomly selected bottle is less than 295 ml?0.15870.99280.84130.00720.0478

Answer 1

Given:

`\begin{gathered} \mu=298ml \\ \sigma=3ml \\ x=295ml \end{gathered}`

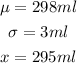
To get the probability, we first need to calculate the Z-score for the data given using the Z-score formula below;

`Z=(x-\mu)/(\sigma)`

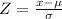
Substituting the given values into the formula;

`\begin{gathered} Z=(295-298)/(3) \\ Z=(-3)/(3) \\ Z=-1 \end{gathered}`

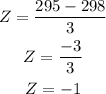
From Z-score tables,

The probability that the content of the selected bottle is less than 295ml is;

[tex]\begin{gathered} P(x<295)=P(x

Therefore, the probability that the content of the selected bottle is less than 295ml is 0.1587