Yvonne has started a business out of her home, where she sells hand-crafted lamp shades. Her weekly income can be modeled by the function p(x) = -2x2 + 75x, where x is the number of lamp shades produced in a week. What is the maximum revenue she earns in a week?
we have that
p(x)=-2x^2+75x -----> is a vertical parabola, open downward
the vertex is a maximum
so
Convert the quadratic equation into vertex form
y=a(x-h)^2+k
where
(h,k) is the vertex
Complete the squares
so
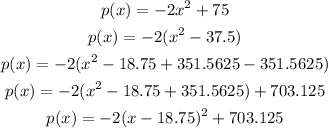
the vertex is the point (18.75,703,125)
therefore
the maximum revenue she earns in a week is $703.13