#(a)
The given function is
![f(x)=3-\sqrt[]{10-2x}](https://img.qammunity.org/2023/formulas/mathematics/college/wn6xkvp6nt8d6vii8su6f5e8l4yhb4dy4m.png)
Since there is no square root for a negative value, then put (10 - 2x) greater than or equal zero to find all values of x can make the function f(x) defined
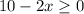
Add 2x to both sides
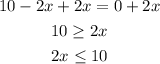
Divide both sides by 2
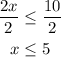
The domain is all values of x less than or equal to 5
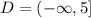
#b)
The given function is
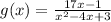
Equate the denominator by 0, then factorize it into 2 factors to find the values of x which make the denominator equal to 0, then exclude these values from the real number
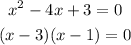
Equate each factor by 0
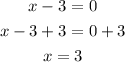
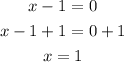
The domain of g(x) is all real numbers except 1 and 3
