The figure is a right triangle since one of its inner angles measures 90°.
Since we are dealing with a right triangle, we can use the following trigonometric identity.
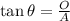
Where theta is an inner angle of the triangle different from the 90°-angle one, O is the opposite side to theta, and A is the adjacent side to that angle.
Therefore, in our case,

Thus,
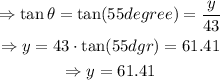
Hence, the answer is y=61.41.