As per given by the question,
There are given that,
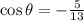
Now,
From the given equation,
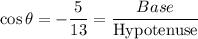
Then,
For finding the sine trigonometric function,

According to the question, there are hypotenuse is given.
Then, need to find the perpendicula with the help of pythagoras theorem.
So,
From the pythagoras theorem,
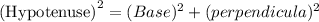
Then,
![\begin{gathered} (\text{Hypotenuse)}^2=(Base)^2+(perpendicula)^2 \\ (13)^2=(-5)^2+(perpendicula)^2 \\ 169=25+(perpendicular)^2 \\ (perpendicular)^2=169-25 \\ (perpendicular)^2=144 \\ perpendicular=\sqrt[]{144} \\ perpendicular=12 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/awxron3na4s5mmn61wfum6hxudvosr3aou.png)
Then,
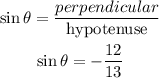
Now,
According to the concept of quadrant, sine and cose function both are negative in third quadrant.
Hence, the option A is correct.