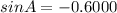Question

Suppose cos(A) = 4/5 Use the trig identity sin^2 (A) + cos^2 (A)= 1 to find sin(A) in quadrant IV. Round to ten-thousandth.-0.39540.64850.4500-0.6000

Answer 1

Given:

`cos\left(A\right)=(4)/(5)`

To find: The angle A lies in the fourth quadrant.

`sinA`

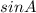
Step-by-step explanation:

Using the trigonometric identity,

`\begin{gathered} sin^2A+cos^2A=1 \\ sin^2A+((4)/(5))^2=1 \\ sin^2A+(16)/(25)=1 \\ sin^2A=1-(16)/(25) \\ sin^2A=(9)/(25) \\ sinA=\pm\sqrt{(9)/(25)} \\ sinA=\pm(3)/(5) \end{gathered}`

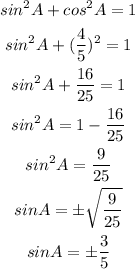
Since the angle lies in the fourth quadrant.

So, the sine value in the fourth quadrant will be negative,

`\begin{gathered} sinA=-(3)/(5) \\ sinA=-0.6000 \end{gathered}`

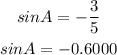
Final answer:

The value of sine of A is,

`sinA=-0.6000`