Question

a total of 1500 middle school students were surveyed. The results showed that 1/4 of the students have a pet living in their homes, 1/5 have a grandparent living in their homes and 1/3 have a baby living in their homes. What is the least possible number of students who have no pets, grandparents or babies living in their homes?

Answer 1

We have a sample of 1500 middle school students.

From the survey we know that:

• 1/4 of the students have a pet

,

• 1/5 have a grandparent

,

• 1/3 have a baby

There is a portion of the students that do not fall into any of this three categories. As we don't know if the categories intersect with each other, we can not know the exact fraction.

But we can know that the minimum fraction of students that do not belong to any of these categories happens if there is no intersection between the categories listed.

This means that the students which have a pet do not have a grandparent or a baby, and so on.

Then, we can calculate the minimum value as 1 minus the sum of the fractions of this three categories:

`\begin{gathered} 1-((1)/(4)+(1)/(5)+(1)/(3)) \\ 1-((15)/(60)+(12)/(60)+(20)/(60)) \\ 1-(47)/(60) \\ (60-47)/(60) \\ (13)/(60) \end{gathered}`

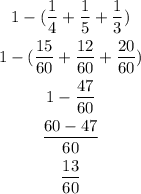
Now that we know the fraction, we can calculate the number of students by multiplying this fraction by 1500:

`n=(13)/(60)\cdot1500=325`

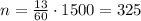
Answer: 325 students.